1.2 Matrices and solutions of systems of simultaneous equations

1.2 Matrices and solutions of systems of simultaneous equations

Matrices

I assume that you are familiar with vectors and matrices and know, in particular, how to multiply them together. (Do the first few exercises to check your knowledge.)

The determinant of the 2 × 2 matrix

a   b   c   d

is ad − bc. If ad − bc ≠ 0, the matrix is nonsingular; in this case its inverse is

1 ad − bc

d   −b   −c   a

.

(You can check that the product of the matrix and its inverse is the identity matrix.) We denote the inverse of the matrix A by A⁻¹.

The determinant of the 3 × 3 matrix

a   b   c  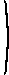 d   e    f    g   h   i

is

Δ = a(ei − h f ) − b(di − g f ) + c(dh − eg).

If Δ ≠ 0 the matrix is nonsingular; in this case its inverse is

1 Δ	D11   −D12   D13  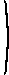 −D21   D22   −D23   D31   −D32   D33

where D_ij is the determinant of the 2 × 2 matrix obtained by deleting the ith column and jth row of the original 3 × 3 matrix. That is, D₁₁ = ei − h f , D₁₂ = bi − ch, D₁₃ = b f  − ec, D₂₁ = di −  f g, D₂₂ = ai −cg, D₂₃ = a f  − dc, D₃₁ = dh − eg, D₃₂ = ah − bg, and D₃₃ = ae − db. (Again, you can check that the product of the matrix and its inverse is the identity matrix.)

The determinant of the matrix A is denoted |A|.

Let A be an n × m matrix (i.e. a matrix with n rows and m columns). The transpose A' of A is the m × n matrix in which, for i = 1, ..., n, the ith row of A' is the ith column of A. In particular, if x is a column vector (n × 1 matrix) then x' is a row vector (1 × n matrix).

Solutions of systems of simultaneous equations

Consider a system of two equations in two variables x and y:

ax + by	= u
cx + dy	= v.

Here are three ways to solve for x and y.

1. Isolate one of the variables in one of the equations and substitute the result into the other equation. For example, from the second equation we have

   y = (v − cx)/d.

   Substituting this expression for y into the first equation yields

   ax + b(v − cx)/d = u,

   which we can write as

   (a − bc/d)x + bv/d = u,

   so that

   x =	u − bv/d a − bc/d

   or

   x =

   ud − bv ad − bc

   .

   To find y we now use the fact that y = (v − cx)/d, to get

   y =

   va − cu ad − bc

   .

2. Use Cramer's rule (due to Gabriel Cramer, 1704-1752). Write the two equations in matrix form as

   a    b   c    d

   x   y

   =

   u   v

   (*)

   Cramer's rule says that the solutions are given by

   x =	u   b   v   d     ad − bc

   and

   y =

   a   u   c   v     ad − bc

   .

   Note that the denominator in these expressions, ad − bc, is the determinant of the matrix at the left of (*). The matrix in the numerator of each expression is obtained by replacing the column in the matrix on the left of (*) that corresponds to the variable for which we are solving with the column vector on the right of (*).Calculating the determinants in the numerators, we have
   

   x =

   ud − bv ad − bc

   and

   y =

   va − cu ad − bc

   .

3. Write the two equations in matrix form as

   a    b   c    d

   x   y

   =

   u   v

   (as when using Cramer's rule) and solve by inverting the matrix on the left hand side. The inverse of this matrix is

   1 ad − bc

   d    −b   −c    a

   so we have

   x   y

   =

   1 ad − bc

   d    −b    −c    a

   u   v

   so that

   x =

   ud − bv ad − bc

   and

   y =

   va − cu ad − bc

   .

Which of these three methods is best depends on several factors, including your ability to remember Cramer's rule and/or how to invert a matrix. If you have to solve for only one of the variables, Cramer's rule is particularly convenient (if you can remember it).

For a system of more than two variables, the same three methods are available. The first method, however, is pretty messy, and unless you are adept at inverting matrices, Cramer's rule is probably your best bet.