Intervals and functions

1.3 Intervals and functions

Intervals

An interval is a set of (real) numbers between, and possibly including, two numbers. The interval from a to b is denoted as follows:

• [a, b] if a and b are included (i.e. [a, b] = {x: a ≤ x ≤ b})
• (a, b) if neither a nor b is included (i.e. (a, b) = {x: a < x < b})
• [a, b) if a is included but b is not
• (a, b] if b is included but a is not.

We use the special symbol "∞" ("infinity") in the notation for intervals that extend indefinitely in one or both directions, as illustrated in the following examples.

• (a, ∞) is the interval {x: a < x}.
• (−∞, a] is the interval {x: x ≤ a}.
• (−∞, ∞) is the set of all numbers.

Note that ∞ is not a number, but simply a symbol we use in the notation for intervals that have at most one endpoint. We alternatively denote the set (−∞, ∞) of all (real) numbers by the symbol ℝ.

The notation (a, b) is used also for an ordered pair of numbers. The fact that the notation has two meanings is unfortunate, but the intended meaning is usually clear from the context. (If it is not, complain to the author.)

The interior of an interval is the set of all numbers in the interval except the endpoints. Thus the interior of [a, b] is (a, b); the interval (a, b) is the interior also of the intervals (a, b], [a, b), and (a, b).

We say that (a, b), which does not contain its endpoints, is an open interval, whereas [a, b], which does contain its endpoints, is a closed interval. The intervals (a, b] and [a, b) are neither open nor closed.

Functions

A function is a rule that associates with every member of some set, a single member of another set. The first set is called the domain of the function. A function with domain A is said to be defined on A.

To specify a function we need to specify the domain and the rule. Here are some examples.

• Domain: [−2, 1]. Rule:  f (x) = x².
• Domain: (−∞, ∞). Rule:  f (x) = x².
• Domain: (−1, 1). Rule:  f (x) = x if x ≥ 0;  f (x) = 1/x if x < 0.
• Domain: union of (0, 1) and (4, 6). Rule:  f (x) = √x.
• Domain: set of all pairs of numbers. Rule:  f (x, y) = xy.
• Domain: set of n-vectors (x₁, ..., x_n) for which 0 ≤ x_i ≤ 1 for i = 1, ..., n. Rule:  f (x₁, ..., x_n) = ∑_i=1ⁿa_ix_i, where a₁, ..., a_n are nonnegative constants.

(Note that the symbols x and y are arbitrary. We could, for example, define the first function equally well by  f (z) = z² or  f (g) = g². We generally use x and y for variables, but we may use any other symbols.)

These examples have two features in common:

• the domain is a subset of the set of n-vectors of numbers, for some positive integer n (where n may of course be 1, as in the first four examples)
• the rule associates a real number with each point in the domain.

A function is not restricted to have these features. For example, the domain of a function may be a set of complex numbers and the function may associate a set with each member of its domain. All the functions in this tutorial, however, have the two features, and the word "function" throughout means a rule that associates a number with every point in some subset of the set of n-vectors of numbers (where n may be 1). I refer to a function whose domain is a set of 1-vectors (i.e. numbers) as a function of a single variable, and one whose domain is a set of n-vectors for n ≥ 1 as a function of many variables. (Note that a function of a single variable is a special case of a function of many variables.)

The number that a function associates with a given member x of its domain is called the value of the function at x. As x varies over all points in the domain of a function, the value of the function may (and generally does) vary. The set of all such values of the function is called the range of the function. Here are the ranges of the examples given above.

• Domain: [−2, 1]. Rule:  f (x) = x². Range: [0, 4].
• Domain: (−∞, ∞). Rule:  f (x) = x². Range: [0, ∞).
• Domain: (−1, 1). Rule:  f (x) = x if x ≥ 0;  f (x) = 1/x if x < 0. Range: union of (−∞, −1) and [0, 1).
• Domain: union of (0, 1) and (4, 6). Rule:  f (x) = √x. Range: union of (0, 1) and (2, √6).
• Domain: set of all pairs of numbers. Rule:  f (x, y) = xy. Range: (−∞, ∞).
• Domain: set of n-vectors (x₁, ..., x_n) for which 0 ≤ x_i ≤ 1 for i = 1, ..., n. Rule:  f (x₁, ..., x_n) = ∑_i=1ⁿa_ix_i, where a₁, ..., a_n are nonnegative constants. Range: (0, ∑_i=1ⁿa_i).

In formal presentations of mathematical material, the notation  f : A → B is used for a function given by the rule  f  and the domain A whose range is a subset of B. We might say, for example, "consider the function  f : [0, 1] → ℝ defined by  f (x) = √x", or "for every function  f : ℝ → ℝ." (Remember that the symbol ℝ denotes the set of all (real) numbers.) The set B in this notation is called the co-domain ortarget of the function. Note that this set is not part of the definition of the function, and may be larger than the range of the function. When we say, for example, "for every function  f : ℝ → ℝ", we mean every function whose domain is ℝ and whose range is a subset of ℝ.

Graphical illustrations aid the understanding of many functions. A function of a single variable, for example, may be represented on x−y coordinates by plotting, for each value of x, the value of  f (x) on the y-axis. An example is shown in the following figure. In this diagram, the small circle indicates a point excluded from the graph: the value of the function at x₀ is y₀, whereas the value of the function at points slightly greater than x₀ is y₁.

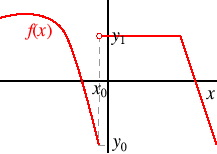
The red line in this figure is called the graph of the function. Techniques for drawing graphs are discussed in a later section.

Logarithms and exponentials

You need to be comfortable working with the logarithm function and with functions of the form x^y (where y is known as an exponent). In particular, you should know the following rules.

• x^yx^z = x^y+z
• (x^y)^z = x^yz (so that in particular (x^y)^1/y = x)
• ln e^x = x and e^ln x = x
• a ln x = ln x^a (so that e^a ln x = x^a)

Continuous functions

A function of a single variable is continuous if its graph has no "jumps", so that it can be drawn without lifting pen from paper. In more precise terms, a function  f  is continuous at the point a if we can ensure that the value  f (x) of the function is as close as we wish to  f (a) by choosing x close enough to a. Here is a completely precise definition for a function of many variables. (The distance between two points (x₁, ..., x_n) and (y₁, ..., y_n) is the Euclidean distance √[∑_i=1ⁿ(x_i − y_i)²].)

Definition Let  f  be a function of many variables and let a be a point in its domain. Then  f  is continuous at a if, for any number ε > 0, there is a number δ > 0 such that for any value of x in the domain of  f  for which the distance between x and a is less than δ, the difference between  f (x) and  f (a) is less than ε. The function  f  is continuous if it is continuous at every point in its domain.

The function whose graph is shown in the previous figure is not continuous at x₀. The value of the function at x₀ is y₀, but the values at points slightly larger than x₀ is much larger than y₀: no matter how small we choose δ, some points x within the distance δ of x₀ yield values of the function far from y₀ (=  f (x₀)).

The following result is useful in determining whether a function is continuous.

Proposition If the functions  f  and g of many variables are continuous at x0 then the function h defined by h(x) =  f (x) + g(x) for all x is continuous at x0. If the functions  f  and g of many variables are continuous at x0 then the function h defined by h(x) =  f (x)g(x) for all x is continuous at x0. If the functions  f  and g of many variables are continuous at x0 and g(x0) ≠ 0 then the function h defined by h(x) =  f (x)/g(x) for all x with g(x) ≠ 0 is continuous at x0. If the function  f  of many variables is continuous at x0 and the function g of a single variable is continuous at  f (x0), then the function h defined by h(x) = g( f (x)) for all x is continuous at x0.

An implication of the second part of this result is that if  f  is continuous at x₀ then the function h defined by h(x) = ( f (x))^k, where k is a positive integer, is continuous at x₀.

A polynomial is a function of a single variable x of the form a₀ + a₁x + a₂x² + ... + a_kx^k, where k is a nonnegative integer and a₀, ..., a_k are any numbers. Because the function  f  defined by  f (x) = x for all xis continuous, all polynomials are continuous.

The next result gives an important property of continuous functions. It says that if the function f of a single variable on the domain [a, b] is continuous, then f(x) takes on every value from f(a) to f(b).

Proposition (Intermediate value theorem) If  f  is a continuous function of a single variable with domain [a,b] and  f (a) ≠  f (b), then for any number y between  f (a) and  f (b), or equal to  f (a) or  f (b), there is a value of x (in [a,b]) such that  f (x) = y.

This result is illustrated in the following figure.

In this figure, the set of values from  f (a) to  f (b) is shown in red; for every value y in this set, there is a value of x such that  f (x) = y. For example,  f (x₁) = y₁. Two points to note:

• For some values y between  f (a) and  f (b) there may be more than one value of x such that y =  f (x). For example, in the figure  f (x₂) =  f (x₃) =  f (x₄) = y₂.
• The result does not say that for values y less than  f (a) or greater than  f (b) there is no x such that  f (x) = y. Indeed, in the figure we have  f (x₅) = y₃.

An important implication of the result is that if  f (a) is positive and  f (b) is negative, then  f (x) = 0 for some x.

Example Consider the function  f  defined by  f (x) = x4 − 4x2 + 2. Does the equation  f (x) = 0 have a solution between 0 and 1? The function is a polynomial, and thus is continuous. We have  f (0) = 2 and  f (1) = −1, so the Intermediate Value Theorem implies that the answer to the question is yes: for some value of x between 0 and 1 we have  f (x) = 0.