Calculus: one variable

1.4 Calculus: one variable

Differentiation

Let  f  be a function of a single variable defined on an open interval. This function is differentiable at the point a if it has a well-defined tangent at a. Its derivative at a, denoted  f '(a), is the slope of this tangent.

Precisely, consider "secant lines" like the one from (a,  f (a)) to (a + h,  f (a + h)) in the following figure.

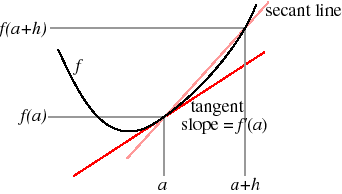
Such a line has slope ( f (a + h) −  f (a))/h. The derivative of  f  at a is defined to be the limit, if it exists, of this slope as h decreases to zero.

Definition The function  f  of a single variable defined on an open interval is differentiable at a if limh→0( f (a + h) −  f (a))/h exists, in which case this limit is the derivative of the function  f  at a, denoted  f '(a).

The statement "lim_h→0( f (a + h) −  f (a))/h exists" means, precisely, that there is a number k such that for every number ε > 0 (no matter how small), we can find a number δ > 0 such that if |h| < δ then the difference between  f (a + h) −  f (a))/h and k is less than ε.

If  f  is differentiable at every point in some interval I, we say that  f  is "differentiable on I".

The graph of a function differentiable at a is "smooth" at a. In particular, a function that is differentiable at a is definitely continuous at a. An example of a function that is not differentiable at some point is shown in the following figure.

The function  f  in the figure is not differentiable at a, because the slope of the secant line from (a,  f (a)) to (a + h,  f (a + h)) is very different for h > 0 and for h < 0, even when h is arbitrarily small, so that lim_h→0( f (a + h) −  f (a))/h does not exist.

At any point at which a function has a "kink", it is similarly not differentiable.

The derivative of  f  at a is sometimes denoted (d f /dx)(a).

Rules for differentiation

The definition of a derivative implies the following formulas for the derivative of specific functions, where a and k are constants.

f (x)		f '(x)
k		0
kxn		knxk−1
ln x		1/x
ex		ex
ax		axln a
cos x		−sin x
sin x		cos x
tan x		1 + (tan x)2

Three general rules (very important!!):

Sum rule

F (x) =  f (x) + g(x): F '(x) =  f '(x) + g'(x)

Product rule

F (x) =  f (x)g(x): F '(x) =  f '(x)g(x) +  f (x)g'(x)

Quotient rule

F (x) =  f (x)/g(x): F '(x) = [ f '(x)g(x) −  f (x)g'(x)]/(g(x))²

Note that if you know that the derivative of (g(x))ⁿ is n(g(x))ⁿ⁻¹g'(x) (an implication of the "chain rule", discussed later), the quotient rule follows directly from the product rule: if you write  f (x)/g(x) as  f (x)(g(x))⁻¹ then the product rule implies that the derivative is

 f '(x)(g(x))⁻¹ −  f (x)(g(x))⁻²g'(x),

which is equal to [ f '(x)g(x) −  f (x)g'(x)]/(g(x))².

Example Let F (x) = x2 + ln x. By the sum rule, F '(x) = 2x + 1/x.

Example Let F (x) = x2ln x. By the product rule, F '(x) = 2xln x + x2/x = 2xln x + x.

Example Let F (x) = x2/ln x. By the quotient rule, F '(x) = [2xln x − x2/x]/(ln x)2 = [2xln x − x]/(ln x)2.

Second derivatives

If the function  f  is differentiable at every point in some open interval I then its derivative  f ' may itself be differentiable at points in this interval. If  f ' is differentiable at x then we say that  f  is twice-differentiable, we call its derivative at x the second derivative of  f  at x, and we denote this derivative  f "(x).

Integration

Let  f  be a function of a single variable on the domain [a, b]. The definition of the ("definite") integral of  f  from a to b, denoted

∫^b_a f (z)dz,

is a measure of the area between the horizontal axis and the graph of  f , between a and b.

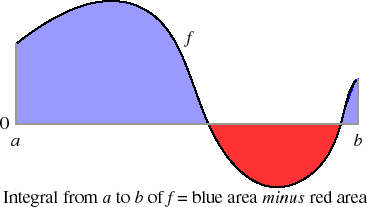
Notes

• If  f (x) < 0 for some x between a and b, then the corresponding areas (shaded red in the above figure) count negatively in the integral.
• The integral is defined precisely as the limit, if it exists, of approximations to the area consisting of sums of the areas of narrow rectangles as the width of these rectangles approaches zero. If the limit exists then  f  is integrable. It may be shown that if  f  is continuous then it is integrable. If  f  is not integrable, then its integral is not defined. (Such functions are fairly exotic. An example is the function  f  with domain [0, 1] defined by  f (x) = 1 if x is a rational number and  f (x) = 0 if x is an irrational number.)
• Note that the variable z is a dummy variable, and can be replaced by any other variable. Sometimes it is dropped entirely, and the integral is written simply as ∫^b_a f .

The fundamental theorem of calculus shows that integration and differentiation are, in a sense, inverse operations.

Proposition (Fundamental theorem of calculus) Let  f  be an integrable function of a single variable defined on [a, b]. Define the function F  of a single variable on the domain [a, b] by F (x) = ∫xa f (z)dz. If  f  is continuous at the point c in [a, b], then F  is differentiable at c and F '(c) =  f (c). Similarly, define the function G on [a, b] by G(x) = ∫bx f (z)dz. If  f  is continuous at the point c in [a, b], then G is differentiable at c and G'(c) = − f (c). If  f  is continuous on [a, b] and  f  = F ' for some function F , then ∫ba f (z)dz = F (b) − F (a).

This result shows us how to calculate the integral of a function  f : we need to find a function that, when differentiated, yields  f .

The symbol

∫ f (x)dx,

called the indefinite integral of  f , denotes the set of functions F  for which F ' =  f . Why "set"? Because if F '(z) =  f (z) for all z then for any function H with H(z) = F (z) + c, where c is a constant, we also have H'(z) =  f (z) for all z. In honor of the constant c, we sometimes write statements like "∫2x dx = x² + c", meaning that the derivative of the function x² + c, for any value of c, is 2x.

For many functions, finding the indefinite integral is not easy. In fact, the integral of many functions cannot be written as an explicit formula.

Some integrals that may be expressed simply are

∫xⁿdx = x^{n + 1}/(n+1) + c,

∫e^xdx = e^x + c

and

∫(1/x)dx = ln |x| + c.

A useful fact to employ when finding some integrals is that the derivative of ln f (x) is  f '(x)/ f (x) (an implication of the chain rule, discussed later). Thus if you can express the function you are integrating in the form  f '(x)/ f (x), its integral is ln f (x). For example,

∫

x x2 + 1

dx = (1/2)ln (x2 + 1) + c.

Integration by parts

We can find the indefinite integral of some functions by using the result that

∫ f (x)g'(x)dx =  f (x)g(x) − ∫ f '(x)g(x)dx.

This result follows from the product rule for differentiation. Define the function h by h(x) =  f (x)g(x) for all x. Then h'(x) =  f '(x)g(x) +  f (x)g'(x), so that h(x) =  f (x)g(x) = ∫ f '(x)g(x)dx + ∫ f (x)g'(x)dx.

This result is useful if we can express the function we want to integrate as a product  f (x)g'(x) with the property that we can easily find the integral  f '(x)g(x). The following example illustrates this point.

Example ∫xexdx = xex − ∫exdx = xex − ex + c. We cannot integrate xex directly, but we can integrate the product of the derivative of x (namely 1) and the integral of ex (namely ex), because that product is simplyex.

The same formula may be used to calculate the definite integral of a function:

∫_a^b f (x)g'(x)dx =  f (a)g(a) −  f (b)g(b) − ∫_a^b f '(x)g(x)dx.